drawing 3d triangle between 3 points
Area of Triangle in Coordinate Geometry
In Geometry, a triangle is a iii-sided polygon that has iii edges and three vertices. The area of the triangle is the space covered by the triangle in a two-dimensional plane. The formula for the area of a triangle is (ane/two) × base × altitude. Let's observe out the area of a triangle in coordinate geometry.
| 1. | What Is the Area of a Triangle in Coordinate Geometry? |
| two. | How Do You lot Calculate the Expanse of A Triangle in Coordinate Geometry? |
| 3. | Area of a Triangle Using Determinants |
| 4. | FAQs on Surface area of a Triangle in Coordinate Geometry |
What Is the Area of a Triangle in Coordinate Geometry?
Coordinate geometry is divers equally the study of geometry using coordinate points. The area of a triangle in coordinate geometry can be calculated if the three vertices of the triangle are given in the coordinate plane. The area of a triangle in coordinate geometry is defined equally the area or space covered by it in the 2-D coordinate plane. Let united states sympathize the concept of the surface area of a triangle in coordinate geometry better using the instance given below,
Consider these three points: A(−2,1), B(3,2), C(1,5). If you plot these iii points in the plane, you will find that they are non-collinear, which means that they can exist the vertices of a triangle, equally shown beneath:
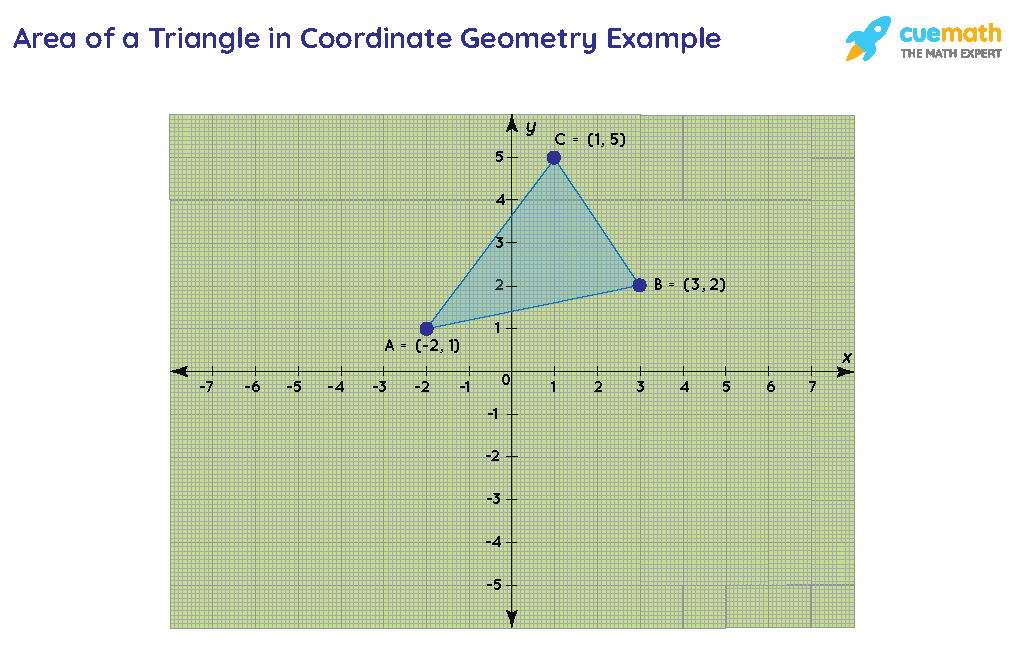
The area covered past the triangle ABC in the 10-y plane is the region marked in blue. At present, with the help of coordinate geometry, we can detect the surface area of this triangle. Let u.s. acquire more nigh information technology in the following department.
How Practise You Summate the Area of A Triangle in Coordinate Geometry?
In coordinate geometry, if we demand to notice the area of a triangle, we utilize the coordinates of the three vertices. Consider ▵ABC equally given in the effigy beneath with vertices A(x1, yone), B(ten\(_2\), y\(_2\)), and C(ten\(_3\), y\(_3\)). In this figure, we take drawn perpendiculars AE, CF, and BD from the vertices of the triangle to the horizontal axis. Detect that three trapeziums are formed: BAED, ACFE, and BCFD.

We can limited the expanse of a triangle in terms of the areas of these three trapeziums.
Area(ΔABC) = Area(Trap.BAED) + Area(Trap.ACFE) - Area(Trap.BCFD)
Now, the area of a trapezium in terms of the lengths of the parallel sides (the bases of the trapezium) and the distance betwixt the parallel sides (the pinnacle of the trapezium):
Trapezium Area = (one/ii) × Sum of bases × Tiptop
Consider any one trapezium, say BAED. Its bases are BD and AE, and its acme is DE. BD and AE tin hands exist seen to be the y coordinates of B and A, while DE is the difference between the 10 coordinates of A and B. Similarly, the bases and heights of the other two trapeziums tin can be easily calculated. Thus, nosotros accept:
Area(Trap.BAED) = (1/2) × (BD + AE) × DE
= (1/two) × (y\(_2\) + y\(_1\)) × (ten\(_1\) − x\(_2\))
Area(Trap.ACFE) = (1/ii) × (AE + CF) × EF
= (ane/2) × (y\(_1\) + y\(_3\)) × (x\(_3\) − x\(_1\))
Area(Trap.BCFD) = (i/ii) × (BD + CF) × DF
= (1/2) × (y\(_2\) + y\(_3\)) × (10\(_3\) − x\(_2\))
The expression for the area of the triangle in terms of the coordinates of its vertices can thus be given as,
Area(ΔABC) = Area(Trap.BAED) + Area(Trap.ACFE) - Area(Trap.BCFD)
= (1/2) × [(y\(_2\) + y\(_1\)) × (x\(_1\) − x\(_2\))] + (1/2) × [(y\(_1\) + y\(_3\)) × (x\(_3\) − x\(_1\))] - (one/2) × [(y\(_2\) + y\(_3\)) × (x\(_3\) − x\(_2\))]
However, we should attempt to simplify it then that it is like shooting fish in a barrel to recall.
For that, we simplify the product of the two brackets in each terms:
= (one/2) (x\(_1\)y\(_2\) − x\(_2\)y\(_2\) + 10\(_1\)y\(_1\) − ten\(_2\)y\(_1\)) + (1/2) (x\(_3\) y\(_1\) − x\(_1\)y\(_1\) + ten\(_3\)y\(_3\) − x\(_1\)y\(_3\)) − (i/two)(x\(_3\)y\(_2\) − x\(_2\)y\(_2\) + ten\(_3\)y\(_3\) − x\(_2\)y\(_3\))
Take the common term i/2 exterior the subclass.
=(one/2) (x\(_1\)y\(_2\) − x\(_2\)y\(_2\) + x\(_1\)y\(_1\) − x\(_2\)y\(_1\) − x\(_3\) y\(_1\) − x\(_1\)y\(_1\) + ten\(_3\)y\(_3\) − x\(_1\)y\(_3\) − 10\(_3\)y\(_2\) + x\(_2\)y\(_2\) - x\(_3\)y\(_3\) + 10\(_2\)y\(_3\))
Thus,
Area(ΔABC) = (1/2){x\(_1\)(y\(_2\) − y\(_3\)) + x\(_2\)(y\(_3\) − y\(_1\)) + ten\(_3\)(y\(_1\) − y\(_2\))}
As the area is ever positive.
(ΔABC) = (ane/two) |x\(_1\)(y\(_2\) − y\(_3\)) + x\(_2\)(y\(_3\) − y\(_1\)) + x\(_3\)(y\(_1\) − y\(_2\))|
This is a symmetric expression, and there is an easy technique to remember it, which we will now talk over as Determinants Method.
Area of a Triangle Using Determinant Method
To summate the area of a triangle using determinants, we use the formula every bit shown below,
Area = one/2 \(\begin{bmatrix}{{x_1}}&{{y_1}}&{{one}}\\{{x_2}}&{{y_2}}&{{1}}\\{x_3}&{y_3}&ane\end{bmatrix}\)
Permit us solve the above expression to obtain the formula for the area of a triangle using coordinates. We will solve the determinant along the commencement column.
At present, the commencement term in the expression for the area is \({x_1}\left( {{y_2} - {y_3}} \right)\). To obtain this, we solve determinants for the first term in the starting time column. Ignore the terms in the outset row and column other than the first term and proceed according to the post-obit visual representation (the cross arrows represent multiplication). Solving determinant we get, ten\(_1\)(y\(_2\) - y\(_3\)).

The second term in the expression for the area is x\(_2\)(y\(_3\) − y\(_1\)). To obtain this, we solve determinant for the second term in the first column. Ignore the terms in the second row and first column other than the first term in the second column. Solving determinant, we get -x\(_2\)(y\(_1\) - y\(_3\)) = ten\(_2\)(\({y_3} - {y_1}\)):

Adjacent, the third term in the expression for the expanse is \({x_3}\left( {{y_1} - {y_2}} \right)\). To obtain this, nosotros solve determinant for the third term in the first column. Ignore the terms in the start row and third column other than the get-go term in the third column:

Finally, we add these 3 terms to get the expanse (and divided by a factor of ii, because nosotros had this gene in the original expression we determined):
Area = (1/2) |x\(_1\)(y\(_2\) − y\(_3\)) + x\(_2\)(y\(_3\) − y\(_1\)) + x\(_3\)(y\(_1\) − y\(_2\))|
Note that we take put a modulus sign (vertical bars) around our algebraic expression, and removed the negative sign because the area is always positive, which we obtained in the original expression. So fifty-fifty if we get a negative value through the algebraic expression, the modulus sign will ensure that it gets converted to a positive value.
We tin write the above expression for area compactly every bit follows:
\(A = \frac{one}{2}\;\left| {\begin{array}{*{20}{c}}{{x_1}}&{{y_1}}&{{ane}}\\{{x_2}}&{{y_2}}&{{1}}\\{x_3}&{y_3}&1\stop{assortment}} \right|\)
Important Notes:
- The surface area of a triangle cannot exist negative. In example we get the answer in negative terms, we should consider the numerical value of the surface area, without the negative sign.
- To find the surface area of a triangle in coordinate geometry, we need to find the length of three sides of a triangle using the distance formula.
-
If 3 points A(ten\(_1\),y\(_1\)), B(x\(_2\),y\(_2\)), and C(x\(_3\),y\(_3\)) are collinear, so x\(_1\)(y\(_2\) − y\(_3\)) + x\(_2\)(y\(_3\) − y\(_1\)) + x\(_3\)(y\(_1\) − y\(_2\)) = 0.
Challenging Questions
- If the altitude between the points (2, 3) and (1, q) is five, detect the values of q.
- What is the formula for the surface area of quadrilateral in coordinate geometry?
Examples on Expanse of a Triangle in Coordinate Geometry
go to slidego to slidego to slide

Breakup tough concepts through simple visuals.
Math will no longer exist a tough bailiwick, especially when yous understand the concepts through visualizations.
Book a Free Trial Form
Practice Questions on Expanse of a Triangle in Coordinate Geometry
go to slidego to slidego to slide
FAQs on Area of a Triangle in Coordinate Geometry
How Exercise You Find the Length of Side of a Triangle Using Coordinates?
The distance formula is used to observe the length of a triangle using coordinates. Altitude formula can be used to find the length of any side given the coordinates of the triangle'southward vertices.
What Is the Formula of the Expanse of a Triangle in Coordinate Geometry?
The formula of area of triangle formula in coordinate geometry the area of triangle in coordinate geometry is: A = (i/2) |x\(_1\)(y\(_2\) − y\(_3\)) + 10\(_2\)(y\(_3\) − y\(_1\)) + x\(_3\)(y\(_1\) − y\(_2\))|, where (x\(_1\),y\(_1\)),(x\(_2\),y\(_2\)), and (ten\(_3\),y\(_3\)) are the coordinates of vertices of triangle.
How Practise You Notice the Surface area and Perimeter of a Triangle With Coordinates?
For the area and perimeter of a triangle with coordinates beginning, we have to find the distance between each pair of points by distance formula and so we apply the formula for surface area and perimeter.
How Do You Detect the Area of a Triangle With three Coordinates?
Expanse of triangle with 3 points is: A = (1/two) |ten\(_1\)(y\(_2\) − y\(_3\)) + 10\(_2\)(y\(_3\) − y\(_1\)) + ten\(_3\)(y\(_1\) − y\(_2\))|, where (x\(_1\),y\(_1\)),(x\(_2\),y\(_2\)), and (x\(_3\),y\(_3\)) are the coordinates of vertices of triangle.
How Do You lot Find the Expanse of Triangle Using Vertices?
The formula of the area of triangle in coordinate geometry is: A = (ane/ii)|x\(_1\)(y\(_2\) − y\(_3\)) + x\(_2\)(y\(_3\) − y\(_1\)) + x\(_3\)(y\(_1\) − y\(_2\))|, where (10\(_1\),y\(_1\)), (ten\(_2\),y\(_2\)), and (x\(_3\),y\(_3\)) are the vertices of triangle.
How Do You Find the Surface area of an Isosceles Triangle Using Coordinates?
First, we use the distance formula to calculate the length of each side of the triangle. If two sides are equal then it'south an isosceles triangle. We tin apply the area of an isosceles triangle formula using the side lengths.
How Do You Find the Area of a Right-Angled Triangle Using Coordinates?
First, we apply the distance formula to calculate the length of each side of the triangle. If the squares of the smaller two distances equal the square of the largest distance, and so these points are the vertices of a correct triangle. or we can use the Pythagoras theorem. Nosotros can utilise the area of a right triangle formula using side lengths.
How Do Yous Calculate the Area of a Triangle on a Graph?
The surface area of a triangle on a graph is calculated by the formula of area which is: A = (1/2) |x\(_1\)(y\(_2\) − y\(_3\)) + x\(_2\)(y\(_3\) − y\(_1\)) + 10\(_3\)(y\(_1\) − y\(_2\))|, where (ten\(_1\),y\(_1\)), (x\(_2\),y\(_2\)), and (x\(_3\),y\(_3\)) are the vertices of triangle.
How Practise Yous Find the Missing Coordinate of a Right-Angled Triangle?
We use the distance formula and Pythagoras theorem to summate the missing coordinate of a right-angled triangle.
Source: https://www.cuemath.com/geometry/area-of-triangle-in-coordinate-geometry/
0 Response to "drawing 3d triangle between 3 points"
Post a Comment